Limit x mendekati adalah konsep penting dalam kalkulus yang berkaitan dengan bagaimana suatu fungsi berperilaku ketika nilai input (x) mendekati suatu nilai tertentu. Memahami konsep ini merupakan kunci untuk memahami turunan, integral, dan berbagai konsep lanjutan lainnya dalam matematika. Artikel ini akan membahas limit x mendekati secara detail, mulai dari definisi hingga penerapannya dalam berbagai permasalahan.
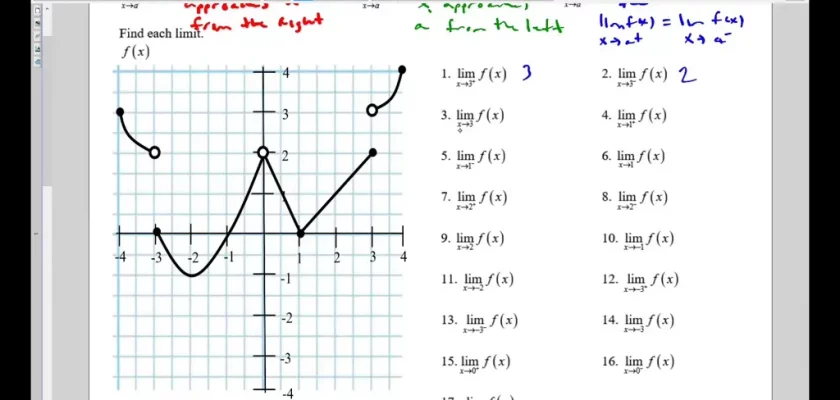
Konsep limit x mendekati berkaitan erat dengan ide pendekatan suatu nilai. Bayangkan kita memiliki sebuah fungsi f(x). Ketika kita ingin mengetahui limit fungsi tersebut ketika x mendekati nilai tertentu, misalnya ‘a’, kita mengamati nilai f(x) saat x semakin mendekati ‘a’, baik dari kiri maupun dari kanan. Nilai limit tersebut adalah nilai yang didekati oleh f(x) ketika x mendekati ‘a’.
Meskipun x mungkin tidak pernah benar-benar sama dengan ‘a’, kita tertarik pada nilai yang didekati oleh f(x) saat x semakin dekat ke ‘a’. Ini penting karena beberapa fungsi memiliki nilai yang tidak terdefinisi pada titik tertentu, namun limitnya masih ada. Sebagai contoh, fungsi f(x) = (x² – 1) / (x – 1) tidak terdefinisi pada x = 1, karena penyebutnya akan menjadi nol. Namun, limit x mendekati 1 untuk fungsi ini ada dan sama dengan 2.
Menghitung Limit x Mendekati
Ada beberapa teknik untuk menghitung limit x mendekati suatu nilai. Teknik yang paling sederhana adalah dengan substitusi langsung. Jika fungsi f(x) kontinu pada titik x = a, maka limitnya dapat dihitung dengan mengganti x dengan a dalam fungsi tersebut. Namun, jika fungsi tersebut tidak kontinu pada titik x = a, kita perlu menggunakan teknik lain seperti pemfaktoran, perkalian dengan konjugat, atau aturan L’Hôpital (untuk limit yang menghasilkan bentuk tak tentu).
Contoh Perhitungan Limit
Mari kita lihat beberapa contoh untuk memahami bagaimana menghitung limit x mendekati:
- Limit x mendekati 2 dari f(x) = x² + 1. Dalam kasus ini, kita dapat menggunakan substitusi langsung: limx→2 (x² + 1) = 2² + 1 = 5
- Limit x mendekati 1 dari f(x) = (x² – 1) / (x – 1). Substitusi langsung menghasilkan bentuk tak tentu 0/0. Kita dapat memfaktorkan pembilang: (x² – 1) = (x – 1)(x + 1). Maka, limitnya menjadi limx→1 (x – 1)(x + 1) / (x – 1) = limx→1 (x + 1) = 2
Dalam contoh kedua, kita menghilangkan faktor (x – 1) dari pembilang dan penyebut, sehingga kita dapat menghitung limitnya.
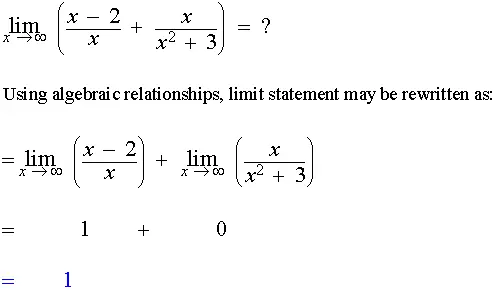
Limit Kiri dan Limit Kanan
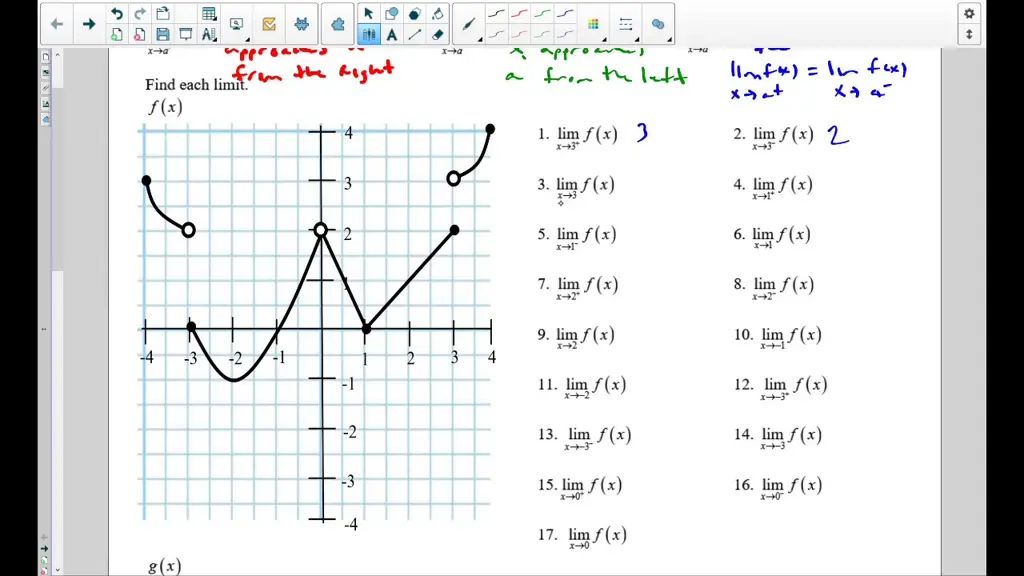
Penting untuk memahami konsep limit kiri dan limit kanan. Limit kiri adalah nilai yang didekati oleh f(x) ketika x mendekati ‘a’ dari kiri (x < a), sedangkan limit kanan adalah nilai yang didekati oleh f(x) ketika x mendekati ‘a’ dari kanan (x > a). Suatu limit dikatakan ada jika dan hanya jika limit kiri dan limit kanan sama.
Limit Tak Hingga
Selain limit x mendekati suatu nilai tertentu, kita juga dapat mempelajari limit x mendekati tak hingga (∞) atau minus tak hingga (-∞). Konsep ini digunakan untuk menganalisis perilaku fungsi ketika nilai input menjadi sangat besar atau sangat kecil.
Penerapan Limit x Mendekati
Konsep limit x mendekati memiliki banyak penerapan dalam berbagai bidang, termasuk:
- Kalkulus: Limit merupakan dasar dari turunan dan integral, yang digunakan untuk menyelesaikan berbagai permasalahan dalam fisika, teknik, dan ekonomi.
- Fisika: Limit digunakan untuk menghitung kecepatan sesaat, percepatan, dan berbagai besaran fisika lainnya.
- Ekonomi: Limit digunakan dalam analisis ekonomi untuk mempelajari perilaku pasar dan memprediksi tren.
Memahami konsep limit x mendekati secara mendalam sangat penting bagi siapa pun yang ingin mempelajari kalkulus dan penerapannya dalam berbagai bidang. Konsep ini mungkin tampak rumit pada awalnya, namun dengan latihan dan pemahaman yang cukup, Anda akan dapat menguasainya.
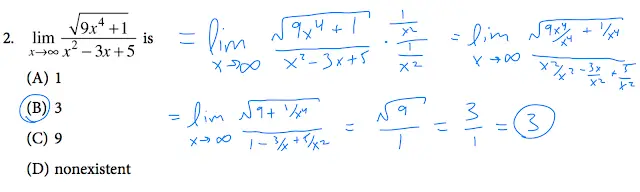
Dengan demikian, memahami limit x mendekati merupakan fondasi yang kuat untuk melangkah lebih jauh dalam mempelajari matematika tingkat lanjut dan aplikasinya di berbagai bidang ilmu. Semoga artikel ini memberikan pemahaman yang lebih baik tentang konsep limit x mendekati dan berbagai teknik yang digunakan untuk menghitungnya.
Untuk memperdalam pemahaman Anda, cobalah untuk mengerjakan soal-soal latihan dan konsultasikan dengan sumber belajar lain seperti buku teks kalkulus atau situs web pendidikan online.